FiltersDone

Question type

Essay

Multiple Choice

Short Answer

True False

Matching

Exam 7: Techniques of Integration

Show Answer

Share

---

All types

Filters

Study Flashcards

Question 21

Multiple Choice

Review LaterAdd Note

Review Later

Use a table of integrals to evaluate the integral. $\int x ^ { 3 } \sin \left( x ^ { 2 } + 3 \right) d x$

A) $\frac { 1 } { 2 } \sin \left( x ^ { 2 } + \sqrt { 3 } \right) - \frac { 1 } { 2 } x ^ { 2 } \cos \left( x ^ { 2 } + \sqrt { 3 } \right) + C$
B) $\frac { 1 } { 2 } \sin \left( x ^ { 2 } + 3 \right) - \frac { 1 } { 2 } x ^ { 2 } \cos \left( x ^ { 2 } + 3 \right) + C$
C) $- \frac { 1 } { 2 } \sin \left( x ^ { 2 } + \sqrt { 3 } \right) - \frac { 1 } { 2 } x ^ { 2 } \cos \left( x ^ { 2 } + \sqrt { 3 } \right) + C$
D) $- \frac { 1 } { 2 } \sin \left( x ^ { 2 } + 3 \right) - \frac { 1 } { 2 } x ^ { 2 } \cos \left( x ^ { 2 } + 3 \right) + C$

E) B) and C)
F) A) and B)

Correct Answer

verified

Show Answer

Question 22

Multiple Choice

Review LaterAdd Note

Review Later

The region $\left\{ ( x + y ) \mid x \geq - 7,0 \leq y \leq e ^ { - x / 5 } \right\}$ is represented below. Find the area of this region to two decimal places.

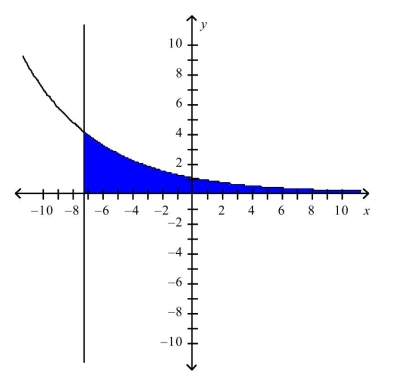
A) $20.28$
B) $17.89$
C) $16.08$
D) $15.89$
E) $15.87$

F) A) and D)
G) C) and D)

Correct Answer

verified

Show Answer

Question 23

Short Answer

Review LaterAdd Note

Find the integral. $\int \frac { d x } { x ( x - 2 ) }$

Evaluate the integral using the indicated trigonometric substitution. $\int \frac { x ^ { 3 } } { \sqrt { x ^ { 2 } + 25 } } d x ; \quad x = 5 \tan \theta$

Evaluate the integral using an appropriate trigonometric substitution. $\int _ { 1 } ^ { 3 } \frac { \sqrt { x ^ { 2 } - 1 } } { x ^ { 4 } } d x$

Evaluate the integral. $\int _ { 2 } ^ { \infty } \frac { d y } { y ^ { 2 } + 2 y - 3 }$

Evaluate the integral or show that it is divergent. $\int _ { - \infty } ^ { \infty } \frac { 5 d x } { 4 x ^ { 2 } + 4 x + 5 }$

Evaluate the integral. $\int _ { 0 } ^ { 4 } \frac { x } { x + 8 } d x$

Find the integral. $\int \frac { x ^ { 3 } - 3 x ^ { 2 } + 6 x - 2 } { x ^ { 3 } - 2 x ^ { 2 } + x } d x$

Make a substitution to express the integrand as a rational function and then evaluate the integral. $\int _ { 4 } ^ { 25 } \frac { \sqrt { x } } { x - 100 } d x$ Round the answer to four decimal places.

Evaluate the integral. $\int _ { 0 } ^ { 1 } 9 x \sin \pi x d x$

Evaluate the indefinite integral. $\int x \cos 9 x d x$

Evaluate the integral. $\int _ { x / 3 } ^ { x / 2 } 2 \cot ^ { 2 } x d x$

Use the Trapezoidal Rule to approximate $\int _ { 2 } ^ { 3 } e ^ { 3 / x } d x$ for $n = 4$ . Round the result to four decimal places.

Find the integral using an appropriate trigonometric substitution. $\int x \sqrt { 16 - x ^ { 2 } } d x$

Determine whether the improper integral converges or diverges, and if it converges, find its value. $\int _ { \pi / 2 } ^ { 5 \pi / 6 } \frac { \cos x } { \sqrt { 1 - \sin x } } d x$

Evaluate the integral using integration by parts with the indicated choices of $u$ and $d v$ . $\int 6 \theta \cos \theta d \theta , u = 6 \theta , d v = \cos \theta d \theta$

Evaluate the indefinite integral. $\int x \cos 9 x d x$

Use the Table of Integrals to evaluate the integral. $\int e ^ { 6 x } \sin 3 x d x$

Use a table of integrals to evaluate the integral. $\int e ^ { - 7 x } \sin 3 x d x$